Giáo án Hình học Lớp 8 - Tuần 21 - Năm học 2018-2019 - Ngô Thanh Tùng
I. MỤC TIÊU:
1. Kiến thức: Nắm vững công thức tính diện tích các đa giác đơn giản, đặc biệt là cách tính diện tích tam giác và hình thang.
2. Kỹ năng : Biết chia một cách hợp lí đa giác cần tìm diện tích thành nhiều đa giác đơn giản. Biết thực hiện các phép vẽ và đo cần thiết.
3. Thái độ: Rèn tính cẩn thận chính xác khi vẽ, đo, tính.
II CHUẨN BỊ:
*Thầy: Bảng phụ, thước thẳng, eke.
*Trò: Thước thẳng, eke.
III. CÁC BƯỚC LÊN LỚP:
1. Ổn định lớp: (1 phút)
2. Kiểm tra bài cũ: (5 phút)
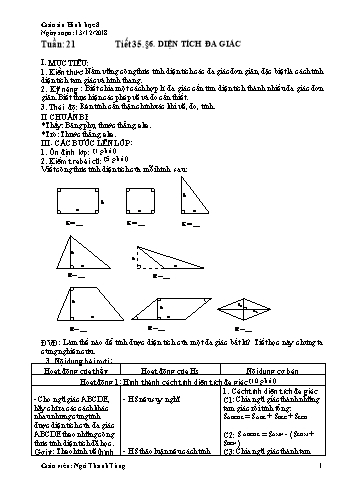
Viết công thức tính diện tích của mỗi hình sau:
Bạn đang xem tài liệu "Giáo án Hình học Lớp 8 - Tuần 21 - Năm học 2018-2019 - Ngô Thanh Tùng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Giáo án Hình học Lớp 8 - Tuần 21 - Năm học 2018-2019 - Ngô Thanh Tùng
Ngày soạn: 13/12/2018 Tuần: 21 Tiết 35. §6. DIỆN TÍCH ĐA GIÁC I. MỤC TIÊU: 1. Kiến thức: Nắm vững công thức tính diện tích các đa giác đơn giản, đặc biệt là cách tính diện tích tam giác và hình thang. 2. Kỹ năng : Biết chia một cách hợp lí đa giác cần tìm diện tích thành nhiều đa giác đơn giản. Biết thực hiện các phép vẽ và đo cần thiết. 3. Thái độ: Rèn tính cẩn thận chính xác khi vẽ, đo, tính. II CHUẨN BỊ: *Thầy: Bảng phụ, thước thẳng, eke. *Trò: Thước thẳng, eke. III. CÁC BƯỚC LÊN LỚP: 1. Ổn định lớp: (1 phút) 2. Kiểm tra bài cũ: (5 phút) Viết công thức tính diện tích của mỗi hình sau: ĐVĐ: Làm thế nào để tính được diện tích của một đa giác bất kì? Tiết học này chúng ta cùng nghiên cứu. 3. Nội dung bài mới: Hoạt động của thầy Hoạt động của Hs Nội dung cơ bản Hoạt động 1: Hình thành cách tính diện tích đa giác (10 phút) - Cho ngũ giác ABCDE, hãy chỉ ra các cách khác nhau nhưng cùng tính được diện tích của đa giác ABCDE theo những công thức tính diện tích đã học. Gợi ý: Theo hình vẽ (hình 148) ta có thể tính diện tích ngũ giác đó thông qua tính diện tích đa giác nào? Vì sao? *Lưu ý: các đa giác đó không có điểm trong chung. - Muốn tính diện tích một đa giác bất kỳ ta làm như thế nào ? - HS nêu suy nghĩ - HS thảo luận nêu cách tính theo các hình 148 tr 129. - Lớp nhận xét HSK: nêu cách tính chung 1. Cách tính diện tích đa giác C1: Chia ngũ giác thành những tam giác rồi tính tổng: SABCDE = SABE + SBEC+ SECD C2: S ABCDE = SAMN - (SEDM + SBCN) C3: Chia ngũ giác thành tam giác vuông và hình thang rồi tính tổng (Xem hình 149) * Trong một số trường hợp, để việc tính toán thuận lợi ta có thể chia đa giác thành nhiều tam giác vuông và hình thang vuông. Hoạt động 2: áp dụng (12 phút) I - YCHS tìm hiểu ví dụ, xác định y/c của bài toán? Cách tính diện tích đa giác ABCDEGHI? - Ta nên chia đa giác đã cho thành những hình nào? - Để tính diện tích của những hình này ta cần biết độ dài những đoạn thẳng nào? - YCHS thực hiện phép đo độ dài các đoạn thẳng và tính diện tích đa giác - Theo dõi, nhận xét và củng cố các kiến thức vận dụng - HS tìm hiểu ví dụ theo gợi ý HSK: Ta vẽ thêm đoạn thẳng AH, CG. Vậy đa giác được chia thành 3 hình : - Hình thang vuông CDEG. - Hình chữ nhật ABGH . - Tam giác AIH - HS nêu được: cần biết độ dài DE, CG, AB, AH, IK. - Cá nhân thực hiện Tb-Y: 3 HS lên tính diện tích + Hình thang vuông CDEG. + Hình chữ nhật ABGH. + Tam giác AIH 2.Ví dụ: Thực hiện các phép vẽ và đo cần thiết để tính diện tích hình ABCDEHHI. Kết quả đo CD = 2cm DE = 3cm CG = 5cm AB = 3cm AH = 7cm IK = 3cm SDEGC = SABGH = 3.7 = 21 (cm2) SAIH = (cm2) Þ SABCDEGHI = SDEGC + SABGH + SAIH = 8 + 21 + 10,5 = 39,5 (cm2) Hoạt động 3: Luyện tập (13 phút) - YCHS tìm hiểu đề bài - Tính diện tích đa giác ABCDE như thế nào? - Để tính tam giác, hình thang đó, ta cần xác định các yếu tố nào? - YCHS tính diện tích đa giác hình 152 - GV theo dõi, nhắc nhở cách đo và vận dụng các công thức để tính - YCHS tìm hiểu đề bài xác định các dữ kiện đã cho và bài toán yêu cầu? - Diện tích phần con đường EBGF có dạng hình gì? tính diện tích hình đó như thế nào? - Tính diện tích đám đất còn lại như thế nào? - Chốt lại cách tính diện tích phần còn lại của đám đất - Theo dõi, uốn nắn các sai sót nếu có - HS tìm hiểu đề bài - SABCDE = SABC + SAHE + + SHKDE + SCDH - HS đo độ dài các đoạn thẳng AC, BG, AH, HK, KC, DK và EH - Cá nhân đo độ dài các đoạn thẳng rồi tính diện tích - HS lên bảng t/b lời giải - Cá nhân làm vở và nhận xét Hs đọc đề bài 38 - Cá nhân trả lời - Tứ giác EBGF là hình bình hành, biết 1 cạnh 50 m chiều cao t/ư là 120m. Vận dụng công thức S = a.h. HSK: Diện tích đất còn lại bằng diện tích đám đất hình chữ nhật trừ đi diện tích phần con đường, cần tính diện tích đám đất - HS thảo luận cách giải - HS thực hiện theo hướng dẫn 1. Bài tập 37 trang 130 Kết quả đo: AC = 4,8cm, BG = 1,9cm AH = 0,8cm, HK = 1,8cm, KC = 2,8cm, DK = 2,3cm và EH = 1,5cm Vậy diện tích đa giác ABCDE là - SABCDE = SABC + SAHE + SHKDE + SCDH = ½ AC.BG + ½ AH.HE + ½.HK(HE + DK) + ½ DK.KC = ½.4,8.1,9 + ½.0,8.1,5 + ½.1,8(1,5 + 2,3) + ½.2,2.2,3 = 11,11cm2 2. Bài tập 38 trang 130 Diện tích con đường: SEBGF = 50.120 = 6000 (m2) Diện tích đám đất: SABCD = 150.120 = 18000 (m2) Diện tích đất còn lại: 18000 – 6000 = 12000 (m2) 4. Củng cố: (2 phút) - Hệ thống lại các công thức tính diện tích tam giác, tứ giác đã học. - Lưu ý khi tính diện tích đa giác cần cùng đơn vị 5. Hướng dẫn học sinh tự học, làm bài tập và soạn bài mới ở nhà: (2 phút) - Nắm chắc các C.Thức tính diện tích tam giác, tứ giác đã học và t/c diện tích đa giác - BT 40 trang 131 Hướng dẫn: tỉ lệ 1/10000 có ý nghĩa là 1cm trên bản vẽ tương ứng với 10000cm = 100m trên thực tế; chia đa giác thành H.thang và hình tam giác để tính diện tích (không có điểm trong chung) IV. RÚT KINH NGHIỆM: ...................................................................................................................................................................................................................................................................................................................... ........................................................................................................................................................... Ngày soạn: 13/12/2018 Tuần: 21 Tiết 36. LUYỆN TẬP I. MỤC TIÊU 1. Kiến thức: Củng cố và khắc sâu các công thức tính diện tích điện tích đa giác và các tính chất về diện tích đa giác 2. Kỹ năng: - Vận dụng công thức tính đã học để tính diện tích hình chữ nhật, hình thang, hình thoi, hình tam giác. 3. Thái độ: Rèn tính cẩn thận chính xác và linh hoạt II. CHUẨN BỊ: *Thầy: thước thẳng, eke. *Trò: Thước thẳng, êke. III. CÁC BƯỚC LÊN LỚP: 1. Ổn định lớp: (1 phút) 2. Kiểm tra bài cũ: (5 phút) Tb-Y: Cho hình thang ABCD (AB//CD), AB = 3,5cm, CD = 6,5cm và đường cao AH = 5cm. Tính diện tích hình thang ABCD ĐS: SABCD = 3. Nội dung bài mới Hoạt động của thầy Hoạt động của trò Nội dung cơ bản Hoạt động 1: Lý thuyết (15 phút) - Nhắc lại đa giác lồi? - YCHS làm bài 1tr 131 - Nhận xét, củng cố khái niệm đa giác lồi - YCHS tìm hiểu bài 2 - Tổng số đo các góc của đa giác n cạnh là bao nhiêu? - Đa giác đều là gì? - Mỗi góc của đa giác đều n cạnh có số đo là bao nhiêu - Vận dụng công thức - Nhắc lại các công thức các hình trong bài 3 - Cá nhân trả lời - HS nêu YC đề bài và kiến thức vận dụng trả lời - Cá nhân trả lời. Lớp nhận xét - Lớp nhận xét - Cá nhân tìm hiểu Tb-Y: (n – 2).1800 Tb-Y: trả lời HSK: trả lời - Lớp nhận xét - Cá nhân trả lời (Tb-Y) - Lớp nhận xét I. Lý thuyết - Đa giác lồi 1. a) Hình năm cạnh GHIKL (hình 156) không phải là đa giác lồi vì khi lấy cạnh KL làm bờ đa giác không cùng nằm trong một nửa mặt phẳng b) Hình năm cạnh MNOPQ không phải là đa giác lồi vì khi lấy cạnh OP làm bờ thì đa giác không cùng nằm trong một nửa mặt phẳng c) Hình sáu cạnh RSTVXY làm bờ là đa giác lồi vì lấy bất kỳ cạnh nào làm bờ thì đa giác luôn cùng một nửa mặt phẳng - Tổng số đo các góc của đa giác n cạnh là:(n – 2).1800 2a) Tổng số đo các góc của một đa giác đều 7 cạnh là (7 – 2).1800 = 9000 2b) Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau 2c) Mỗi góc của ngũ giác đều là: 1080 - Mỗi góc của ngũ giác đều là: 1200 - Hình chữ nhật: S = a.b - Hình vuông: S = a2 - Tam giác : S = a.h - Hình thang: S = (a + b).h - Hình bình hành: S = a.h - Hình thoi: S = Hoạt động 2: Bài tập (22 phút) - Xét ∆BDE , ta biết được gì? Nêu cách tính diện tích ∆BDE? (cạnh đáy, chiều cao) - Nêu cách tính diện tích tứ giác EHIK? + Đa giác có thể chia thành các đa giác nào? + = ?, = ?. - Gọi HS lên bảng giải - Theo dõi, nhận xét và cũng cố kiến thức. - Cá nhân trả lời: DE = 6cm, chiều cao BC = 6,8cm - HS thảo luận cách tính theo gợi ý. - Cá nhân làm bài và nhận xét bài làm trên bảng HSK: lên bảng giải Bài 41/132 - Diện tích tam giác BDE = 20,4cm2 - Diện tích tam giác CEH = 10,2cm2 - Diện tích tam giác CIK = 2,55cm2 - Diện tích tứ giác EHIK là cm2 4. Củng cố: ( phút) Củng cố trong luyện tập 5. Hướng dẫn học sinh tự học, làm bài tập và soạn bài mới ở nhà: (2 phút) - Nắm chắc cách tính diện tích của các loại tứ giác đã học trong bài và t/c diện tích của đa giác. - Bài tập 45/133 Hướng dẫn: Dùng công thức tính diện tích hình bình hành Chuẩn bị bài mới: Định lý Ta lét trong tam giác – tỉ số hai đoạn thẳng, định lý Ta lét (GT và KL) IV. RÚT KINH NGHIỆM: ...................................................................................................................................................................................................................................................................................................................... ........................................................................................................................................................... Duyệt của tổ trưởng tuần 21 Ngày 29/12/2018 Trương Thị Ngọc Tiếng
File đính kèm:
 giao_an_hinh_hoc_lop_8_tuan_21_nam_hoc_2018_2019_ngo_thanh_t.doc
giao_an_hinh_hoc_lop_8_tuan_21_nam_hoc_2018_2019_ngo_thanh_t.doc

